未公開企業におけるストック・オプションの取扱い
未公開企業については、ストック・オプションの公正な評価単価に代え、ストック・オプションの単位当たりの本源的価値の見積りに基づいて会計処理を行うことができます(ストック・オプション等に関する会計基準第13項)。
本源的価値の見積りに基づいて会計処理する場合、同会計基準の「公正な評価単価」は「単位当たりの本源的価値」と読み替えて適用します。
ストック・オプションの単位当たりの本源的価値の見積額は、その後は見直しません。
本源的価値と時間的価値
ストック・オプションの行使価格は、そのストック・オプションの持っている価値に支払う対価と言えます。
ストック・オプションにどれだけの価値があるのかという評価には、本源的価値と時間的価値という2つの考え方があります。
本源的価値
本源的価値とは、現時点でオプションを行使したと仮定した場合に市場価格と行使価格との差が利益であるときの価値のことです。
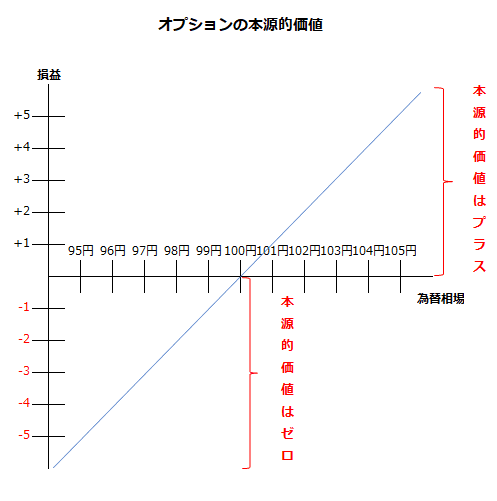
例えば、1ドルを100円で買えるコール・オプション(買う権利)を持っており、現在の為替相場が1ドル=105円だったとします。この場合、コール・オプションを行使して1ドルを100円で取得し、市場で105円で売却すれば、5円の利益が出ます。この5円の利益が、当該コール・オプションの本源的価値です。
現在の為替相場が1ドル=100円だった場合は、コール・オプションの行使価格と同額なので、利益はゼロとなります。したがって、この場合は、本源的価値がゼロとなります。
では、現在の為替相場が1ドル=95円だった場合はどうでしょうか。この場合は、コール・オプションを行使すると5円の損失(95円-100円)となるので、当該コール・オプションの価値は、-5円となりそうです。しかし、オプションは権利であって義務ではないので、オプションを行使して損失が出る場合には、オプションを行使する必要はありません。したがって、オプションの行使で損失が発生する場合にはオプションを行使しないので、当該オプションの本源的価値もゼロとなります。
なお、ストック・オプション等に関する会計基準第13項では、単位当たりの本源的価値を以下のように定義しています。
ここで、「単位当たりの本源的価値」とは、算定時点においてストック・オプションが権利行使されると仮定した場合の単位当たりの価値であり、当該時点におけるストック・オプションの原資産である自社の株式の評価額と行使価格との差額をいう。
時間的価値
時間的価値とは、行使期日までに相場の変動により生まれる可能性があるオプションの価値のことです。
先の例で、行使価格が1ドル=100円のコール・オプションは、現時点での為替相場が100円以下の場合、本源的価値がゼロでした。
しかし、例えば、行使期日がまだ30日あった場合、その間に為替相場は1ドル=100円を超える可能性があります。
このように行使期日までに期間が残されているオプションには、時間的価値があります。そして、時間的価値は、期日が迫って来ると加速度的に減少し、期日に消滅します。
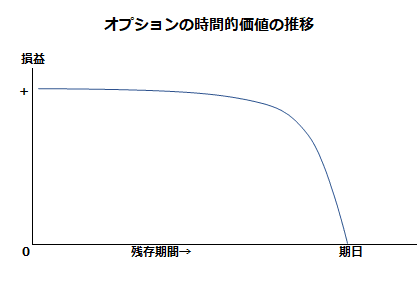
以上のようにオプションには、本源的価値と時間的価値があるので、その価値総額は以下のように表せます。
- オプションの価値 = 本源的価値 + 時間的価値
ストック・オプションの本源的価値の計算
ストック・オプションの本源的価値は、以下の計算式で求めます。
- ストック・オプションの本源的価値
= 自社の株式の評価額 - 行使価格
上記の計算で、ストック・オプションの本源的価値がゼロとなった場合には、人件費と新株予約権は計上されません。
なお、未公開企業が損益計算上は、ストック・オプションの本源的価値による算定を行う場合であっても、その付与日における価値によることとし、その後の見直しは求められていません。
ただし、ストック・オプションの各期末における本源的価値の合計額および各会計期間中に権利行使されたストック・オプションの権利行使日における本源的価値の合計額につき、注記で開示する必要があります(ストック・オプション等に関する会計基準第16項(5)および第63項)。
公開直後の企業の取扱い
公開直後の企業については、以下の理由から、ストック・オプションの本源的価値による算定は認められていません(ストック・オプション等に関する会計基準第63項)。
- 公開後の日は浅くとも自社の株価を参照できる
- 一般投資家のいない未公開企業と同列に考えることはできない
- 仮に公開後の日の浅い企業についてもストック・オプションの本源的価値による算定を認めることとした場合には、その範囲を明確に画する必要があるが、一律にその範囲を画することは困難である
