2種類の製品を製造販売しており、共通的な制約条件が複数ある場合の最適プロダクト・ミックスの計算
ここでは、2種類の製品を製造販売していて、共通的な制約条件が複数ある場合の最適プロダクト・ミックスの計算について、具体例を用いて解説します。
計算の前提
甲社では、A、Bの2種類の製品を継続的に大量生産しています。次期の予算編成に際して、最適プロダクト・ミックスを決定する必要があり、そのために以下の資料を入手しています。
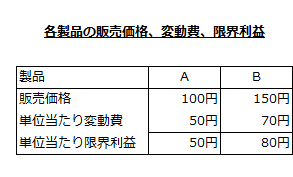
各製品の販売価格、変動費、限界利益
各製品1単位当たりの販売価格、変動費、限界利益は以下の通りです。
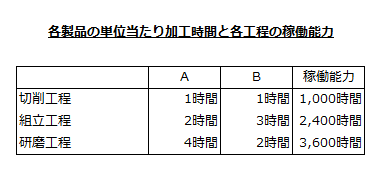
各製品の加工時間と各工程の稼働能力
工程には、切削、組立、研磨の3つがあります。各製品の工程ごとの単位当たり加工時間と各工程の稼働能力は以下の通りです。
固定費
次期の固定費総額は50,000円と見積もっています。
なお、A製品もB製品も販売能力には十分な余裕があり、次期に生産した製品は全て次期に販売可能です。
問題の定式化
2種類の製品を製造販売しており、共通的な制約条件が複数ある場合には、全ての制約条件を満たして利益が最大になる製品の組み合わせをグラフ分析で導き出します。
そのためには、まず問題を定式化しなければなりません。
製品Aをx、製品Bをyとおくと、限界利益を最大化する目的関数は以下のようになります。
50x+80y=z の最大化
ただし、x、yは負の値を取らないので、
非負条件:x,y≧0
切削工程、組立工程、研磨工程には稼働能力に限界があるので、制約条件は以下の通りです。
x + y = 1,000
2x + 3y = 2,400
4x + 2y = 3,600
グラフの作成
次に制約条件をグラフに描きます。
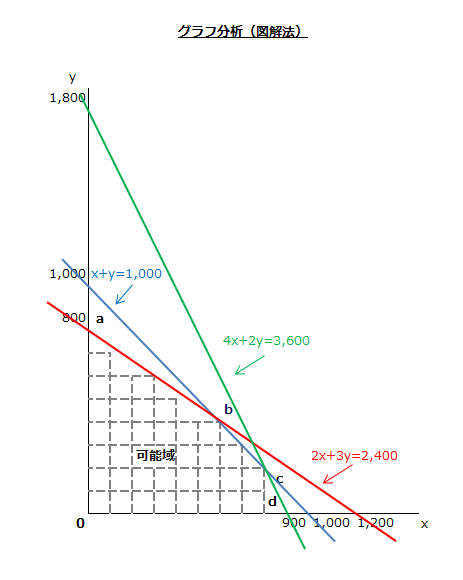
上記のグラフから、点0、a、b、c、dに囲まれた範囲が可能域となります。そして、限界利益が最大となる最適解は、この点0、a、b、c、dのいずれかになります。
点a
点aは、y軸と「2x+3y=2,400」の交点なので、x=0、y=800になります。
- 2×0+3y=2,400
3y=2,400
y=800
点b
点bは、「x+y=1,000」と「2x+3y=2,400」の交点なので、以下の連立方程式を解けば、x=600、y=400になります。

点c
点cは、「x+y=1,000」と「4x+2y=3,600」の交点なので、以下の連立方程式を解けば、x=800、y=200になります。

点d
点dは、x軸と「4x+2y=3,600」の交点なので、x=900、y=0になります。
- 4x+2×0=3,600
4x=3,600
x=900
最適解の決定
以上から、点0、a、b、c、dの各プロダクト・ミックスの限界利益を計算します。
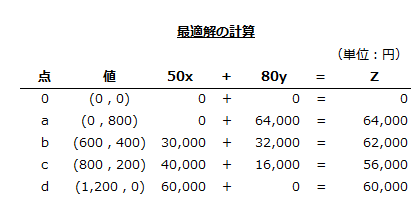
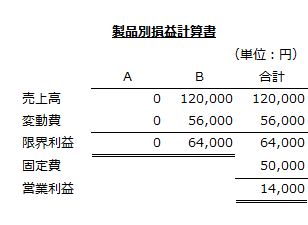
上記より、点aが限界利益64,000円と最も大きいので、A製品0個、B製品800個が最適プロダクト・ミックスになります。
製品別損益計算書
A製品を0個、B製品を800個、製造販売した場合の製品別損益計算書は以下の通りです。