3種類の製品を製造販売しており、共通的な制約条件が複数ある場合の最適プロダクト・ミックスの計算
ここでは、3種類の製品を製造販売していて、共通的な制約条件が複数ある場合の最適プロダクト・ミックスの計算について、具体例を用いて解説します。
計算の前提
甲社では、A、B、Cの3種類の製品を継続的に大量生産しています。次期の予算編成に際して、最適プロダクト・ミックスを決定する必要があり、そのために以下の資料を入手しています。
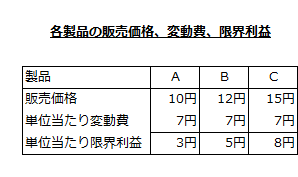
各製品の販売価格、変動費、限界利益
各製品1単位当たりの販売価格、変動費、限界利益は以下の通りです。
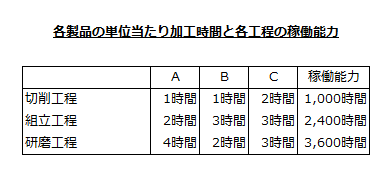
各製品の加工時間と各工程の稼働能力
工程には、切削、組立、研磨の3つがあります。各製品の工程ごとの単位当たり加工時間と各工程の稼働能力は以下の通りです。
固定費
次期の固定費総額は3,000円と見積もっています。
なお、各製品の販売能力には十分な余裕があり、次期に生産した製品は全て次期に販売可能です。
問題の定式化
A製品を「A」、B製品を「B」、C製品を「C」とおき、目的関数、制約条件、非負条件を示すと以下のようになります。
- 目的関数
Z=3A+5B+8Cの最大化 - 制約条件
A+B+2C≦1,000
2A+3B+3C≦2,400
4A+2B+3C≦3,600 - 非負条件
A,B,C≧0
3種類の製品を製造販売しているため、グラフ分析ではなく、シンプレックス法を使って最適プロダクト・ミックスを決定します。
初期基底可能解の決定
制約条件の不等式を消すために各制約式にs₁、s₂、s₃のスラック変数を加えます。また、目的関数の右辺の項を左辺に移項します。
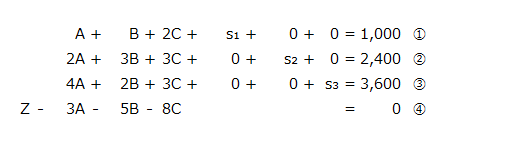
上記式では、A、B、Cの値を0とおいた場合、初期基底可能解は以下のようになります。
s₁=1,000
s₂=2,400
s₃=3,600
Z=0
この場合、目的関数の値Zが0なので、A製品、B製品、C製品を全く生産していません。そして、切削工程の1,000時間、組立工程の2,400時間、研磨工程の3,600時間の稼働能力は、全く使われていない状態です。
シンプレックス法のスタート地点である初期基底可能解は、構造変数を非基底変数とし、スラック変数を基底変数とします。
なお、シンプレックス法では、以下のようなシンプレックス表を作成し、最適解を求めていくのが便利です。
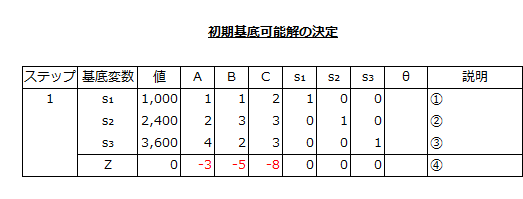
初期基底可能解は、シンプレックス表の最下段の目的関数に負(-)の値が含まれているので、最適解ではありません。
第2の基底可能解の決定
初期基底可能解が最適解ではないとわかったので、解を改良していきます。
基底変数に組入れる非基底変数
シンプレックス表の最下段の目的関数の非基底変数のうち-8が絶対値最大の負の係数なので、基底変数に組み入れる非基底変数はCになります。
非基底変数に入れる基底変数
新しい基底変数がCと定まった後、これをθまで増やすとどうなるかを考えます。この場合でもAとBは0としておきます。
A=0
B=0
C=θ
とおき、①、②、③、④の式を解くと以下のようになります。
s₁=1,000-2θ
s₂=2,400-3θ
s₃=3,600-3θ
Z=8θ
目的関数Z=8θを大きくすることが目的なので、θの値は大きいほど好ましいといえます。しかし、変数には非負条件があるので、θを無限に大きくすることはできません。そのためθの取りうる範囲には限界があり、以下を満たす範囲の値しか取れません。
s₁=1,000-2θ≧0
s₂=2,400-3θ≧0
s₃=3,600-3θ≧0
したがって、Cの取りうる値の限界は以下のようになります。
500≧θ
800≧θ
1,200≧θ
上の式でθが最小のものが非基底変数に入れられます。この場合は、500が最小であり、θ=500のとき、s₁=0となります。したがって、新しい基底変数はs₁になります。
第2の基底可能解の判定
シンプレックス表のθの欄には、s₁=500、s₂=800、s₃=1,200を入れます。
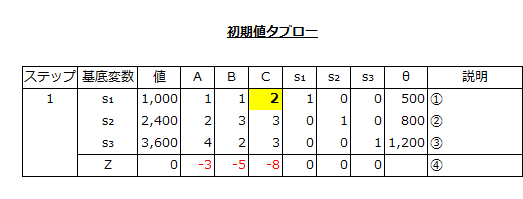
基底変数に組入れる非基底変数はC(絶対値最大の-8)
非基底変数に入れる基底変数はs₁(θが最小の500)
となり、両者が交わっている欄に入っている値2を軸要素(ピボット・エレメント)とします。
次に軸要素を使って、①、②、③、④の式を⑤、⑥、⑦、⑧に変換します。
①を軸要素2で除して⑤とします。②、③、④は、Cの係数が0となるように⑤式を用いて消去の計算をします。
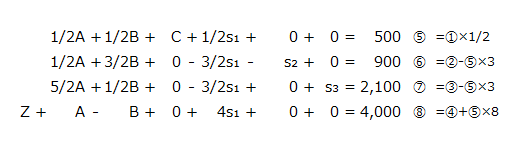
なお、⑥、⑦、⑧の計算は以下の通りです。
⑥の計算
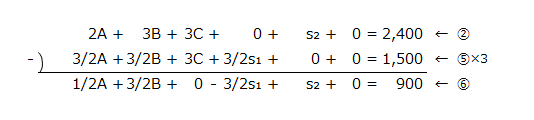
⑦の計算
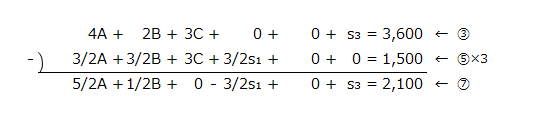
⑧の計算
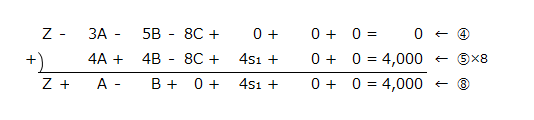
そして、⑤、⑥、⑦、⑧の式をシンプレックス表に記入すると以下のようになります。
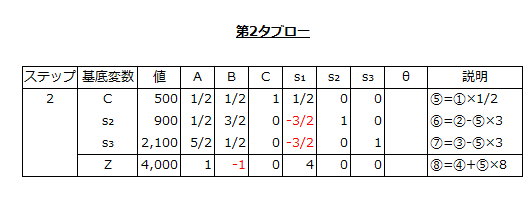
第3の基底可能解の決定
シンプレックス表の3行目で、負(-)の値はBの-1だけなので、基底変数に組み入れる非基底変数はBになります。
非基底変数に入れる基底変数は、以下よりs₂になります。
C=500-1/2θ≧0
s₂=900-3/2θ≧0
s₃=2,100-1/2θ≧0
1,000≧θ
600≧θ
4,200≧θ
以上より、軸要素はBとs₂が交わる欄の3/2になります。
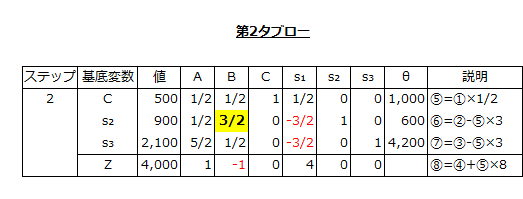
第2の基底可能解を決定した時と同じように軸要素を使って、⑤、⑥、⑦、⑧の式を⑨、⑩、⑪、⑫に変換します。
⑥を軸要素3/2で除して⑩とします。⑨、⑪、⑫は、Bの係数が0となるように⑩式を用いて消去の計算をします。
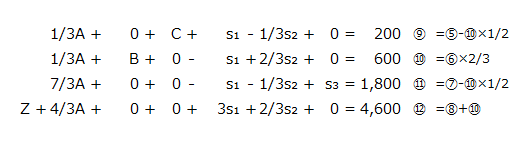
なお、⑨、⑪、⑫の計算は以下の通りです。
⑨の計算
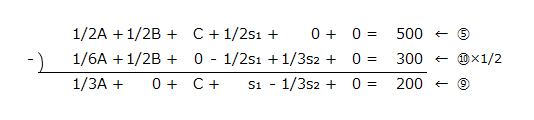
⑪の計算
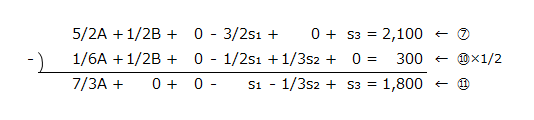
⑫の計算
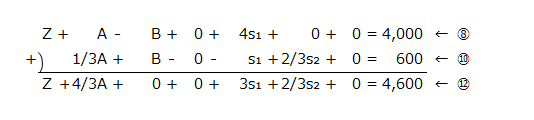
そして、⑨、⑩、⑪、⑫の式をシンプレックス表に記入すると以下のようになります。
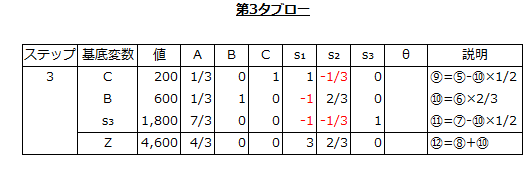
シンプレックス表の最終行の値は、正(+)または0となっており、負(-)はありません。したがって、これが最適解となります。
すなわち、B製品を600個、C製品を200個、生産販売すると限界利益が4,600円得られる計画が、最適プロダクト・ミックスとなります。
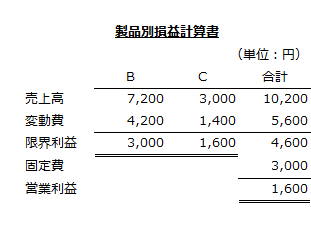
製品別損益計算書
以上より、B製品を600個、C製品を200個製造販売した場合の製品別損益計算書は以下の通りです。
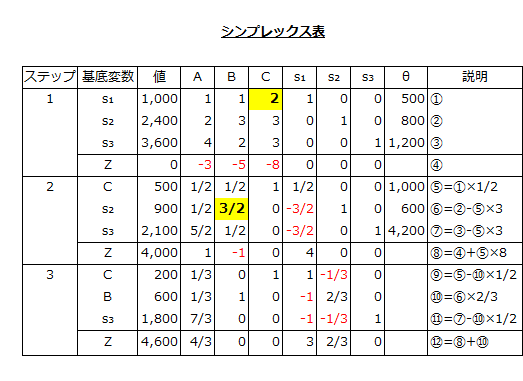
また、初期値タブローから第3タブローまでをまとめたシンプレックス表は以下の通りです。
シャドー・プライス
シンプレックス表の第3タブロー(ステップ3)の最終行のs₁は3、s₂は2/3となっています。
仮に切削工程(s₁)の稼働能力を1時間増やすことができた場合、限界利益は3円増加します。また、組立工程(s₂)の稼働能力を1時間増やすことができた場合、限界利益は2/3円増加します。
研磨工程(s₃)は、これ以上稼働能力を増やしても限界利益は増加しません。
