共通的な制約条件が単一の場合の最適プロダクト・ミックスの計算
ここでは、共通的な制約条件が単一の場合の最適プロダクト・ミックスの計算について、具体例を用いて解説します。
計算の前提
甲社では、A、B、Cの3種類の製品を継続的に大量生産しています。次期の予算編成に際して、最適プロダクト・ミックスを決定する必要があり、そのために以下の資料を入手しています。
各製品の販売価格、変動費、限界利益
各製品1単位当たりの販売価格、変動費、限界利益は以下の通りです。
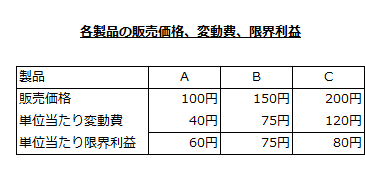
各製品の作業時間、販売能力
各製品の次期に予想される機械作業時間と販売能力は以下の通りです。
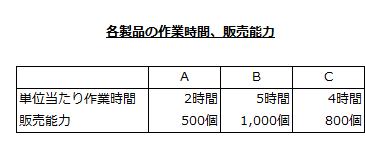
操業度と固定費
次期の操業度は5,000時間、固定費総額は80,000円と見積もっています。
なお、次期の生産量と販売量は等しいと仮定します。
各製品の収益性
甲社では、各製品の製造に要する機械作業時間が共通の制約条件となっています。したがって、各製品の収益性は、機械作業時間当たりの限界利益を指標とします。
- A製品の収益性=60円/2時間=30円/時間
- B製品の収益性=75円/5時間=15円/時間
- C製品の収益性=80円/4時間=20円/時間
機械作業時間当たりの限界利益が最も高いのはA製品なので、A製品のみを製造販売するのが有利となります。
しかし、甲社では、各製品の販売能力に限界があるので、A製品を販売能力の限界まで製造して機械作業時間に余裕がある場合には、2番目に収益性が高いC製品を製造し、なおも機械作業時間に余裕があればB製品を製造すれば、制約条件のもとで営業利益を最大化できます。
各製品の生産量
A製品を販売能力の限界である500個生産すると、機械作業時間が1,000時間必要になります。
- A製品の機械作業時間=2時間×500個=1,000時間
次期に予想される操業度が5,000時間なので、A製品に1,000時間を消費した後の残りの機械作業時間は4,000時間です。
- A製品生産後の残りの機械作業時間
=5,000時間-1,000時間=4,000時間
次にC製品800個を生産するのに3,200時間かかります。
- C製品の機械作業時間=4時間×800個=3,200時間
C製品生産後の残りの機械作業時間は800時間です。
- C製品生産後の残りの機械作業時間
=4,000時間-3,200時間=800時間
B製品は、残りの機械作業時間800時間を使って160個を生産します。
- B製品の生産量=800時間/5時間=160個
B製品の販売能力は1,000個のため、160個生産しても全て販売可能です。
以上より、最適プロダクト・ミックスは以下のようになります。
- A製品=500個
- B製品=160個
- C製品=800個
製品別損益計算書
最適プロダクト・ミックスを計算した後は、製品別予算損益計算書を作成します。
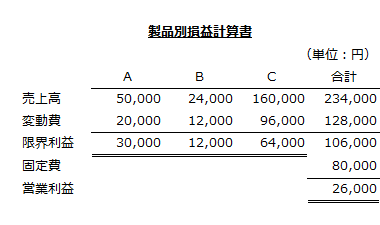
A製品
- 売上高=100円×500個=50,000円
- 変動費=40円×500個=20,000円
- 限界利益=50,000円-20,000円=30,000円
B製品
- 売上高=150円×160個=24,000円
- 変動費=75円×160個=12,000円
- 限界利益=24,000円-12,000円=12,000円
C製品
- 売上高=200円×800個=160,000円
- 変動費=120円×800個=96,000円
- 限界利益=160,000円-96,000円=64,000円
PV図表と損益分岐点売上高
以上の結果からPV図表(限界利益図表)を作成すると以下のようになります。なお、縦軸は金額、横軸は操業度(機械作業時間)です。
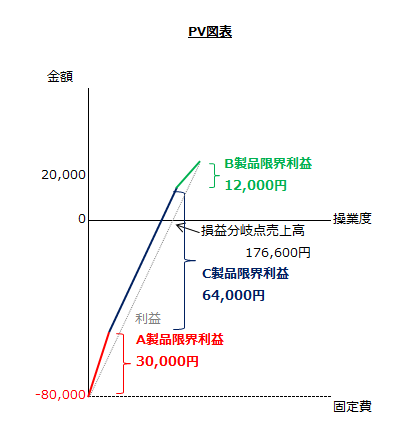
上記PV図表は、機械作業時間が制約条件となっているため、機械作業時間当たりの限界利益が高い順に作図しています。このように作図することで、各製品の利益全体に対して果たしている貢献度がわかりやすくなります。
損益分岐点売上高
損益分岐点売上高は、固定費を加重平均限界利益率で除して計算します。
- 加重平均限界利益率=106,000円/234,000円=0.453
- 損益分岐点売上高=80,000円/0.453=176,600円
