シンプレックス法による最適プロダクト・ミックスの決定
最適プロダクト・ミックスの決定にグラフ分析を用いると視覚的にわかりやすい利点があります。
しかし、グラフ分析の場合、生産販売する製品が3種類以上になると複雑となります。また、制約条件が多くなると、すぐに最適解を見つけるのが困難です。
そこで、製品の種類や制約条件が多く複雑な場合には、比較的簡単に最適プロダクト・ミックスを導くことができるシンプレックス法を用いるのが一般的です。
グラフ分析
まずは簡単な例を使って、グラフ分析から最適プロダクト・ミックスを決定してみましょう。
ある会社が、A製品とB製品を製造販売しており、各製品の販売価格、変動費、限界利益は以下の通りだったとします。
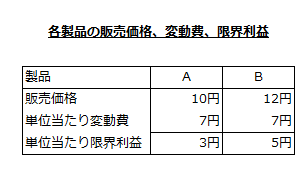
そして、各工程の製品1単位の製造に要する加工時間と稼働能力は以下の通りでした。
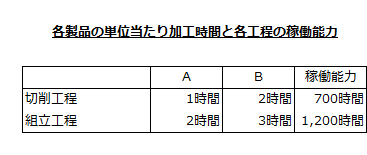
問題の定式化
A製品を「A」、B製品を「B」とおき、目的関数、制約条件、非負条件を示すと以下のようになります。
- 目的関数
Z=3A+5Bの最大化 - 制約条件
A+2B≦700
2A+3B≦1,200 - 非負条件
A,B≧0
グラフの作成
制約条件と非負条件をグラフに書いて、可能域を示します。
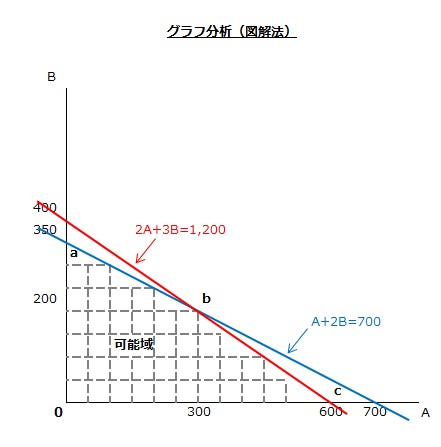
最適解は、点a、b、cのいずれかになります。
点a
点aは、B軸と「A+2B=700」の交点なので、A=0、B=350になります。
- 1×0+2B=700
2B=700
B=350
点b
点bは、「A+2B=700」と「2A+3B=1,200」の交点なので、以下の連立方程式を解けば、A=300、B=200になります。
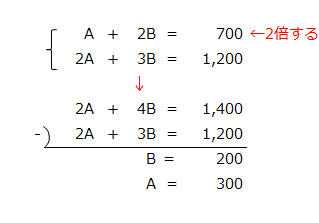
点c
点cは、A軸と「2A+3B=1,200」の交点なので、A=600、B=0になります。
- 2A+3×0=1,200
2A=1,200
A=600
最適解の決定
以上から、点a、b、cの各プロダクト・ミックスの限界利益を計算します。
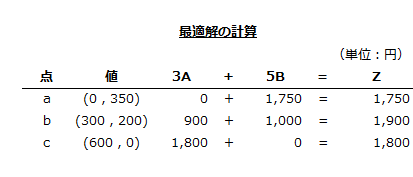
上記より、点bが限界利益1,900円と最も大きいので、A製品300個、B製品200個が最適プロダクト・ミックスになります。
シンプレックス法での最適解の決定
シンプレックス法で最適プロダクト・ミックスを決定する手順は以下の通りです。
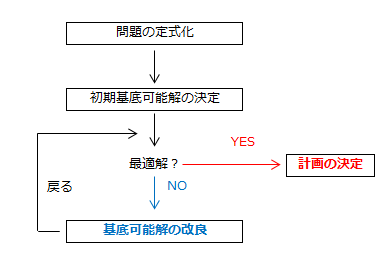
シンプレックス法では、制約条件にスラック変数を加えるところから始まります。
上のグラフ分析で用いた制約条件にs₁、s₂のスラック変数を加えると、以下の2つの等式が得られます。
A+2B+s₁=700
2A+3B+s₂=1,200
この式は、4個の変数に関する2個の1次方程式からなる連立方程式です。そのため、解は一意に定まりません。
そこで、グラフ分析で使ったグラフの端点0、a、b、cにおいて、上記式の各変数がどのような値を取るかを計算します。
例えば、点0であればA=0、B=0とおいて上記式を解けば良く、点aであればA=0、s₁=0とおき、点bであればs₁=0、s₂=0、点cであればB=0、s₂=0とおけば、変数の数と方程式の数が一致するため、解は一意に定まります。
なお、その値を0とおく変数は非基底変数、その後に解かれる変数は基底変数といいます。
各点における変数の値は、以下のようになります。
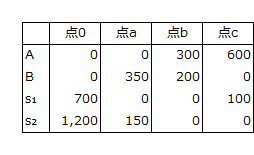
グラフ分析で用いたグラフには、点0、a、b、c以外にも交点がありますが、変数のいずれかがマイナスとなり、非負条件に反しています。したがって、A製品とB製品の可能な組み合わせは、多角形0abcの線上とその内部の可能域の中にあり、この中にある解を可能解といいます。
そして、限界利益を最大にするA製品とB製品の組み合わせは、必ず端点上に存在するので、そのいずれかが最適解となります。
端点に応ずる各変数の値を基底解といい、可能域内に存在する各端点に応ずる各変数を基底可能解といいます。点0、a、b、cは基底可能解であり、そのうち目的関数を最大にする解が最適解です。上の例では、点bに応ずる各変数の値が最適解となります。
グラフ分析では、基底可能解のすべてについて各変数を調べ最適解を見つけ出しました。しかし、このような方法では、変数や制約条件式の数が多くなると手間がかかりすぎますし、場合によっては最適解にたどり着けないこともあります。
そこで考え出されたのが、シンプレックス法です。シンプレックス法なら、基底可能解の中から最適解を探し出すのにグラフ分析のような手間はかかりません。
問題の定式化
グラフ分析での目的関数、制約条件、非負条件は以下の通りでした。
- 目的関数
Z=3A+5Bの最大化 - 制約条件
A+2B≦700
2A+3B≦1,200 - 非負条件
A,B≧0
シンプレックス法で最適解を導き出すためには、まず、制約条件の不等式を等式に変換する必要があります。不等式から等式に変換する際は、以下のルールに従います。
≦の不等式では正(+)のスラック変数を加える
≧の不等式では負(-)のスラック変数を加える
したがって、制約条件の不等式は以下の等式に変換します。
A+2B+s₁=700
2A+3B+s₂=1,200
なお、スラック変数以外の変数を構造変数といいます。
また、目的関数も項を移項して以下のように書きます。
Z-3A-5B=0
スラック変数は、制約値に対する余裕を意味します。
例えば、s₁は、切削工程での加工時間が限界の700時間に達しない場合の余裕を意味しています。
同様にs₂は、組立工程での加工時間が限界の1,200時間に達しない場合の余裕を意味します。
もしも、生産能力を完全に使用できる計画が立てられれば、スラック変数は0になります。
しかし、生産能力を完全に使用できる計画を立てられなければ、スラック変数は正(+)の値を取ります。
また、生産能力に負の余裕はあり得ないので、スラック変数についても非負条件が成立します。
初期基底可能解の決定
もう一度、定式を以下に示します。

連立方程式では、変数が方程式の数よりも多い場合、一般的に解が無数に存在します。そこで、方程式の数を上回った分の変数の値を指定して、他の変数の値を導きます。上記では2個の変数の値を指定することになります。
上記式では、AとBの値を0とおいた場合、初期基底可能解は以下のようになります。
s₁=700
s₂=1,200
Z=0
この場合、目的関数の値Zが0なので、A製品もB製品も全く生産していません。そして、切削工程の700時間、組立工程の1,200時間の稼働能力は、全く使われていない状態です。
これは、グラフ分析で使ったグラフの点0の状態であり、限界利益は0です。
シンプレックス法のスタート地点である初期基底可能解は、構造変数を非基底変数とし、スラック変数を基底変数とします。
なお、シンプレックス法では、以下のようなシンプレックス表を作成し、最適解を求めていくのが便利です。
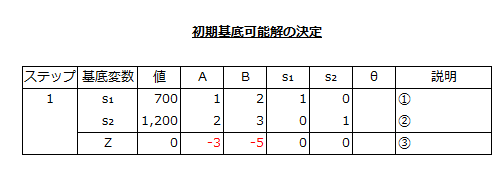
上のシンプレックス表では、①に以下の式の値を入れます。
A+2B+s₁=700
値には700、Aには1、Bには2、s₁には1、s₂には0が入ります。
②には以下の式の値を入れます。
2A+3B+s₂=1,200
そして、③にも同様に以下の式の値を入れます。
Z-3A-5B=0
初期基底可能解が最適解か判定する
初期基底可能解は、A製品を0個、B製品を0個生産する計画なので、すぐに最適解ではないと判断できます。
では、例えば、A製品を10個、B製品を20個生産する計画を立てた場合、これが最適解かどうかをどうやって見分ければ良いでしょうか?
これは、シンプレックス表の基底変数Zを見ればわかります。Aの係数は「-3」、Bの係数は「-5」となっています。
目的関数における非基底変数の係数の符号が負(-)であれば、それは最適解ではありません。最適解は、目的関数のAとBの値が必ず正(+)または0となります。
シンプレックス法では、その解が最適解かどうかを判定し、最適解でなければ、その解を改良していきます。最終的に目的関数に負(-)の値が存在しなくなれば、それが最適解となります。
なお、目的関数における非基底変数の係数の符号は、最適性の判定基準となるため、シンプレックス基準といいます。
第2の基底可能解の決定
初期基底可能解が最適解ではないとわかったので、解を改良していきます。
解を改良するには、非基底変数のいずれかから1つを選び基底変数に組み入れるとともに基底変数のいずれかから1つを選び非基底変数にし、基底可能解を求めます。
基底変数に組入れる非基底変数
新たに基底変数に組み入れる変数の候補が2つ以上ある場合には、目的関数の値をより大きくできる変数を選べば、最短で最適解にたどり着けます。そして、それは、絶対値が最大の負の係数を持つ非基底変数です。
「Z=-3A-5B=0」のAとBの係数では、Bが絶対値最大の負の係数を持っているので、基底変数に組み入れる非基底変数はBになります。
非基底変数に入れる基底変数
新しい基底変数がBと定まった後、これをθまで増やすとどうなるかを考えます。この場合でもAは0としておきます。
A=0
B=θ
とおき、①、②、③の式を解くと以下のようになります。
s₁=700-2θ
s₂=1,200-3θ
Z=5θ
目的関数Z=5θを大きくすることが目的なので、θの値は大きいほど好ましいといえます。しかし、変数には非負条件があるので、θを無限に大きくすることはできません。そのためθの取りうる範囲には限界があり、以下を満たす範囲の値しか取れません。
s₁=700-2θ≧0
s₂=1,200-3θ≧0
したがって、Bの取りうる値の限界は以下のようになります。
350≧θ
400≧θ
上の式でθが最小のものが非基底変数に入れられます。この場合は、350が最小であり、θ=350のとき、s₁=0となります。したがって、新しい基底変数はs₁になります。
第2の基底可能解の判定
シンプレックス表のθの欄には、s₁=350、s₂=400を入れます。
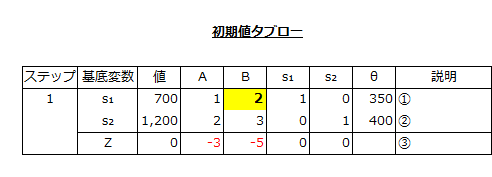
基底変数に組入れる非基底変数はB(絶対値最大の-5)
非基底変数に入れる基底変数はs₁(θが最小の350)
となり、両者が交わっている欄に入っている値2を軸要素(ピボット・エレメント)とします。
次に軸要素を使って、①、②、③の式を④、⑤、⑥に変換します。
①を軸要素2で除して④とします。②と③は、Bの係数が0となるように④式を用いて消去の計算をします。
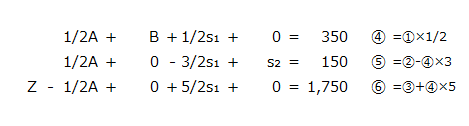
なお、⑤と⑥の計算は以下の通りです。
⑤の計算
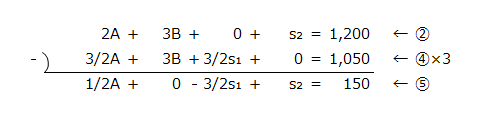
⑥の計算
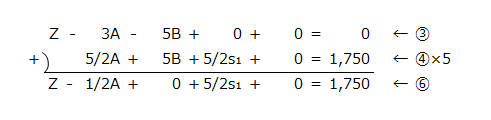
そして、④、⑤、⑥の式をシンプレックス表に記入すると以下のようになります。
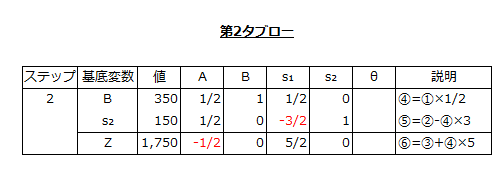
第3の基底可能解の決定
シンプレックス表の3行目で、負(-)の値はAの-1/2だけなので、基底変数に組み入れる非基底変数はAになります。
非基底変数に入れる基底変数は、以下よりs₂になります。
B=350-1/2θ≧0
s₂=150-1/2θ≧0
700≧θ
300≧θ
以上より、軸要素はAとs₂が交わる欄の1/2になります。
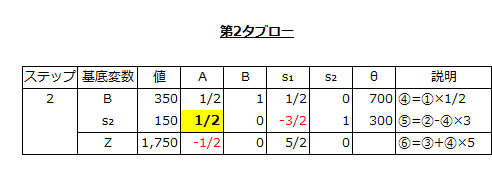
第2の基底可能解を決定した時と同じように軸要素を使って、④、⑤、⑥の式を⑦、⑧、⑨に変換します。
⑤を軸要素1/2で除して⑧とします。⑦と⑨は、Aの係数が0となるように⑧式を用いて消去の計算をします。
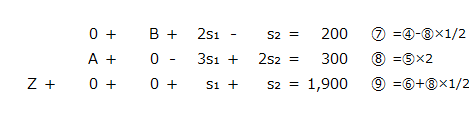
なお、⑦と⑨の計算は以下の通りです。
⑦の計算
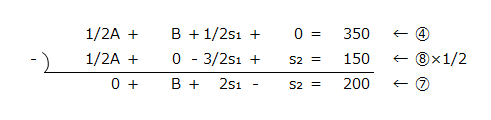
⑨の計算
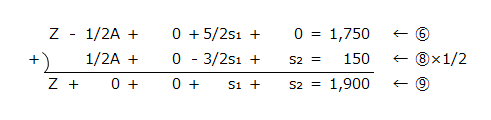
そして、⑦、⑧、⑨の式をシンプレックス表に記入すると以下のようになります。
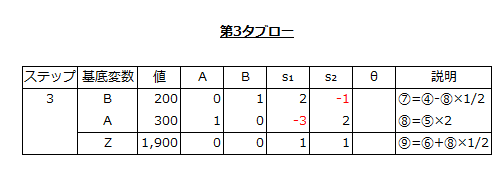
シンプレックス表の3行目の値は、正(+)または0となっており、負(-)はありません。したがって、これが最適解となります。
すなわち、A製品を300個、B製品を200個、生産販売すると限界利益が1,900円得られる計画が、最適プロダクト・ミックスとなります。これは、グラフ分析で導いた最適プロダクト・ミックスと一致しています。
シャドー・プライス
シンプレックス表の第3タブロー(ステップ3)の最終行は
Z+s₁+s₂=1,900
です。
この式は、以下のようにも変形できます。
Z=1,900-s₁-s₂
この式ではs₁(切削工程)の加工時間を1時間減らすと限界利益が1円減少することを意味しています。同様にs₂(組立工程)の加工時間を1時間減らすと限界利益は1円減少します。
反対にs₁(切削工程)の加工時間を1時間増加できれば、限界利益は1円増加します。s₂(組立工程)の加工時間も1時間増加できれば、限界利益は1円増加します。
これらの値は、生産時間1単位が持つ限界生産力を意味しており、シャドー・プライスといいます。
シンプレックス表
初期値タブローから第3タブローまでをまとめたシンプレックス表は以下の通りです。
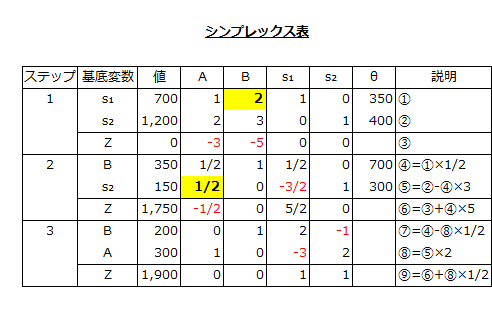
このシンプレックス表を見ると、グラフ分析の点0(0 , 0)、点a(0 , 350)、点b(300 , 200)を順にたどったのと同じになります。
このようにシンプレックス法では、端点における目的関数の値を全て調べなくても、最短経路で最適解を導くことができます。
